ЕГЭ–2026, информатика: задания, ответы, решения

Задания

Версия для печати и копирования в MS Word

Тип 20 № 55816 Добавить в вариант

Для игры, описанной в задании 19, найдите два минимальных значения S, при которых у Пети есть выигрышная стратегия вторым ходом, при этом он не может гарантировано выиграть за один ход.

Ответ:

Спрятать решение

Решение.

Пете необходимо, чтобы Ваня оказался в позиции S  — 19, тогда он сможет выиграть своим вторым ходом, независимо от того, как сходит Ваня.

Рассмотрим значение S  =  18. Своим первым ходом Петя увеличивает количество камней в куче на 1. Тогда Ваня может получить позиции 20, 23 и 76. Во всех случаях Петя увеличивает количество камней в куче в четыре раза и выигрывает своим вторым ходом.

Рассмотрим значение S  =  15. Своим первым ходом Петя увеличивает количество камней в куче на 4. Тогда Ваня может получить позиции 20, 23 и 76. Во всех случаях Петя увеличивает количество камней в куче в четыре раза и выигрывает своим вторым ходом.

Ответ: 15  18.

Приведём решение Юрия Красильникова на языке Python.

def move(n,lim,s):

# n - номер хода, lim - ограничение на число ходов, s - число камней

# Результат: 1 - выиграл первый игрок, 2 - второй, 0 - победителя нет

player = 2 - n%2# Текущий игрок

rival = 3 - player# Противник

if s >= 78:# Игра уже окончена

return rival # Выиграл сделавший предыдущий ход

if n > lim:# Превышен лимит ходов

return 0# Победитель не определен

pos = [s+1, s+4, s*4]# Позиции после хода игрока

res = [move(n+1, lim, x) for x in pos]# Результаты ходов

if any([x == player for x in res]):# Есть выигрышный ход

return player

if all([x == rival for x in res]):# Все ходы проигрышные

return rival

return 0# Победитель не определен

print('#19:',*[s for s in range(1,78) if move(1,2,s)==2])

print('#20:',*[s for s in range(1,78) if move(1,1,s)==0 and move(1,3,s)==1])

print('#21:',*[s for s in range(1,78) if move(1,2,s)==0 and move(1,4,s)==2])

Источник: ЕГЭ по информатике 06.04.2023. Досрочная волна

Спрятать решение · Помощь

Тип 19 № 55815 Добавить в вариант

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня, либо увеличить количество камней в куче в четыре раза. У каждого игрока есть неограниченное количество камней, чтобы делать ходы.

Игра завершается в тот момент, когда количество камней в куче становится не менее 78.

Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу из 78 или более камня.

В начальный момент в куче было S камней; 1 ≤ S ≤ 77.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.

Укажите минимальное значение S, при котором Ваня может выиграть своим первым ходом после любого хода Пети.

Решение.

Такое значение S  — 19. Своим первым ходом Петя может получить позиции 20, 23 и 76. Во всех случаях Ваня увеличивает количество камней в куче в четыре раза и выигрывает своим первым ходом.

Ответ: 19.

Приведём другое решение на языке Python.

Для контроля ходов игроков заведём переменную m.

Если m  =  1, то это действие x + 1.

Если m  =  2, то это действие x + 4.

Если m  =  3, то это действие x · 4.

Таким образом, можно исключать ходы, которые уже были сделаны, не включая их в возвращаемые значения функции.

def f(x, h, m):

if h == 3 and x >= 78:

return 1

elif h == 3 and x < 78:

return 0

elif x >= 78 and h < 3:

return 0

else:

if h % 2 == 0:

if h == 2:

if m == 1:

return f(x + 1, h + 1, m) or f(x * 4, h + 1, m)

elif m == 2:

return f(x + 4, h + 1, m) or f(x * 4, h + 1, m)

elif m == 3:

return f(x + 1, h + 1, m) or f(x + 4, h + 1, m)

else:

return f(x + 1, h + 1, 1) and f(x + 4, h + 1, 2) and f(x * 4, h + 1, 3)

for x in range(1, 78):

if f(x, 1, 0) == 1:

print("Задача 19:", x)

break

Приведём решение Евгения Джобса (аналитическое).

Изобразим игру схематически:

Сперва определим все значения S, при которых ходящий из них игрок может выиграть первым ходом (одним или несколькими из допустимых ходов). Тогда:

$совокупность выражений \text ход плюс 1: S=77, \text ход плюс 4: 74 меньше или равно S меньше или равно 77, \text ход умножить на 4: 20 меньше или равно S меньше или равно 77. конец совокупности .$

Следовательно, при значениях S, принадлежащих диапазону [20; 77], игрок, делающий ход из них одерживает победу своим первым ходом (выигрышные позиции для игры длиной в один ход).

Чтобы найти выигрышные позиции для игры длиной в два хода (вопрос задачи), необходимо, чтобы после первого хода следующий игрок ходил из выигрышной позиции для игры длиной в один ход.

$система выражений 20 меньше или равно S плюс 1 меньше или равно 77, 20 меньше или равно S плюс 4 меньше или равно 77, 20 меньше или равно 4 S меньше или равно 77, S \notin левая квадратная скобка 20; 77 правая квадратная скобка конец системы равносильно система выражений 19 меньше или равно S меньше или равно 76, 16 меньше или равно S меньше или равно 73, 5 меньше или равно S меньше или равно 19, S \notin левая квадратная скобка 20; 77 правая квадратная скобка конец системы . равносильно S=19.$

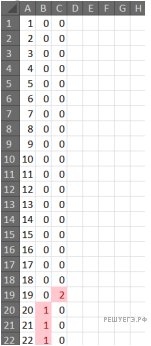
Приведём решение Евгения Джобса (электронные таблицы, формула).

Вставим в столбец А с ячейки A1 числа арифметической прогрессии от 1 до 78 с шагом 1.

В ячейке В1 запишем формулу для победы первым ходом В1:

=ЕСЛИ(ИЛИ(А1+1>79;A1+4>79;A1*4>79);1;0).

В ячейке C1 запишем формулу для победы вторым ходом:

B1 =ЕСЛИ(ИЛИ(A1+1>79;A1+4>79;A1*4>79);1;0).

Условие B1  =  1 гарантирует, что проверяемое значение не удовлетворяло игре в один ход. ИНДЕКС(В:В;А1*4) возвращает значение для 4S в столбце В. Также для удобства поиска найденных значений наложим на диапазон B:Е условное форматирование для значений неравных 0.

Приведём решение Юрия Красильникова на языке Python.

def move(n,lim,s):

# n - номер хода, lim - ограничение на число ходов, s - число камней

# Результат: 1 - выиграл первый игрок, 2 - второй, 0 - победителя нет

player = 2 - n%2# Текущий игрок

rival = 3 - player# Противник

if s >= 78:# Игра уже окончена

return rival # Выиграл сделавший предыдущий ход

if n > lim:# Превышен лимит ходов

return 0# Победитель не определен

pos = [s+1, s+4, s*4]# Позиции после хода игрока

res = [move(n+1, lim, x) for x in pos]# Результаты ходов

if any([x == player for x in res]):# Есть выигрышный ход

return player

if all([x == rival for x in res]):# Все ходы проигрышные

return rival

return 0# Победитель не определен

print('#19:',*[s for s in range(1,78) if move(1,2,s)==2])

print('#20:',*[s for s in range(1,78) if move(1,1,s)==0 and move(1,3,s)==1])

print('#21:',*[s for s in range(1,78) if move(1,2,s)==0 and move(1,4,s)==2])

Источник: ЕГЭ по информатике 06.04.2023. Досрочная волна

Решение · Помощь

Тип 21 № 55817 Добавить в вариант

Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:

—  у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

—  у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Решение.

Такое значение S  — 14. При S  =  14 Петя своим первым ходом может получить позиции 15, 18 и 56.

Рассмотрим значение S  =  15. Своим первым ходом Ваня увеличивает количество камней в куче на 4. Тогда Петя может получить позиции 20, 23 и 76. Во всех случаях Ваня увеличивает количество камней в куче в 4 раза и выигрывает.

Рассмотрим значение S   =  18. Своим первым ходом Ваня увеличивает количество камней в куче на 1. Тогда Петя может получить позиции 20, 23 и 76. Во всех случаях Ваня увеличивает количество камней в куче в 4 раза и выигрывает.

Рассмотрим значение S  =  56. Своим первым ходом Ваня увеличивает количество камней в 4 раза и выигрывает.

Ответ: 14.

Приведём решение Евгения Джобса (аналитическое).

Изобразим игру схематически, опираясь на данные, которые нашли при решении предыдущей задачи.

То есть необходимо, чтобы ход из позиции для S был либо в значения 15 или 18, либо в позицию с количеством камней от 20 до 77. При этом значение S не должно входить в уже найденные множества для задач 19 и 20. Получаем:

$система выражений совокупность выражений S плюс 1=15, S плюс 1=18, S плюс 1 больше или равно 20, конец системы . совокупность выражений S плюс 4=15, S плюс 4=18, S плюс 4 больше или равно 20, конец совокупности . совокупность выражений S=4=15, S умножить на 4=18, S умножить на 4 больше или равно 20 конец совокупности . конец совокупности . равносильно система выражений совокупность выражений S=14,S=17, S больше или равно 19, конец системы . совокупность выражений S=11,S=14, S больше или равно 16 конец совокупности . S больше или равно 5 конец совокупности . равносильно совокупность выражений S=14,S=17. конец совокупности .$

Приведём решение Евгения Джобса (ручное, эл. таблицы).

В первой строке укажем количество камней в куче.

Во второй строке последовательно закрасим сначала клетки, соответствующие игре в один ход (зеленый), затем в два (красный). После этого найдем ячейки, которые соответствуют игре в три хода (зеленый 2) и игре в 4 хода (красный 2).

Приведём решение Евгения Джобса на языке Python.

Так как мы будем находить победу вторым или четвертым ходом, необходимо ограничить перебор значений условием, что перебираемое значение не входит в множество s2.

# множество вершин для игры в 1 ход

s1 = set()

for s in range(1, 77):

if any(x >= 78 for x in (s+1, s+4, s*4)):

s1.add(s)

# множество вершин для игры в 2 хода

s2 = set()

for s in range(1, 77):

if all(x in s1 for x in (s+1, s+4, s*4)):

s2.add(s)

# множество вершин для игры в 3 хода

s3 = set()

for s in range(1, 77):

if all(x in s2 for x in (s+1, s+4, s*4)):

s3.add(s)

# множество вершин для четвертого хода

s4 = set()

for s in range(1, 77):

if s not in s2 and\

all(x in s1|s3 for x in (s+1, s+4, s*4)):

s4.add(s)

print(min(s4))

Приведём решение Юрия Красильникова на языке Python.

def move(n,lim,s):

# n - номер хода, lim - ограничение на число ходов, s - число камней

# Результат: 1 - выиграл первый игрок, 2 - второй, 0 - победителя нет

player = 2 - n%2# Текущий игрок

rival = 3 - player# Противник

if s >= 78:# Игра уже окончена

return rival # Выиграл сделавший предыдущий ход

if n > lim:# Превышен лимит ходов

return 0# Победитель не определен

pos = [s+1, s+4, s*4]# Позиции после хода игрока

res = [move(n+1, lim, x) for x in pos]# Результаты ходов

if any([x == player for x in res]):# Есть выигрышный ход

return player

if all([x == rival for x in res]):# Все ходы проигрышные

return rival

return 0# Победитель не определен

print('#19:',*[s for s in range(1,78) if move(1,2,s)==2])

print('#20:',*[s for s in range(1,78) if move(1,1,s)==0 and move(1,3,s)==1])

print('#21:',*[s for s in range(1,78) if move(1,2,s)==0 and move(1,4,s)==2])

Источник: ЕГЭ по информатике 06.04.2023. Досрочная волна

Решение · Помощь