Тип 21 № 63037 
Выигрышная стратегия. Задание 3. Одна куча
i
Для игры, описанной в задании 19, найдите наибольшее значение S, при котором у Вани есть стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволила бы ему гарантированно выиграть первым ходом.
Решение. Такое значение S — 56. Своим первым ходом Петя может получить позиции 57 или 84 (так как число делится на 2). В случае позиции 84 Ваня выигрывает своим первым ходом (так как 84 делится на 2). Если Петя делает позицию 57, Ваня может получить позиции 58 или 76. В случае позиции 76 выиграет Петя, поэтому Ваня делает позицию 58. В случае позиции 58, Петя может получить позиции 59 или 87. В позиции 59 Ваня удваивает количество камней, а в позиции 87 добавляет треть камней в куче и выигрывает своим первым ходом.
Приведём решение на языке Python.
def f(x, h):
if x >= 96:
return h % 2 == 0
if h == 0:
return 0
c = [f(x + 1, h - 1)]
if x % 2 == 0:
c += [f(x *3 // 2, h - 1)]
if x % 3 == 0:
c += [f(x *4 // 3, h - 1)]
if x % 2 != 0 and x % 3 != 0:
c += [f(x * 2, h - 1)]
return any (c) if h % 2 != 0 else all(c)
for x in range(96,1,-1):
if f(x, 4) == 1 and f(x, 2) == 0:
print("Задача 21: ", x)
break
Решим задание с помощью электронных таблиц.
Скопируем решение задачи 19 шестнадцать раз начиная с ячейки M3. Там где было начальное количество камней в куче будет ход Пети, а где был ход Пети, будет ход Вани. Меняем значения в ячейках:
В ячейку M3 — ход =L3+1.
В ячейку M67 — ход =ЕСЛИ(ОСТАТ(L3;2)=0;L3+L3*0,5;-1000).
В ячейку M131 — ход =ЕСЛИ(ОСТАТ(L3;3)=0;L3+L3*1/3;-1000).
В ячейку M195 — ход =ЕСЛИ(И(ОСТАТ(L3;2)<>0;ОСТАТ(L3;3)<>0);L3*2;-1000).
Меняя значение в ячейке G3, добиваемся такого результата, когда у Пети будут зеленые ячейки в строках, соответствующих ходам Вани.
Получим следующую таблицу и подходящее значение 56: решение.xlsx.
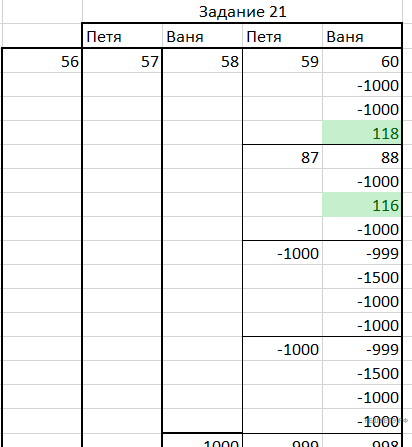
Ответ: 56.
Ответ: 56
 PDF-версии:
PDF-версии: 