Решение. Отсортируем данные в таблице так, чтобы все независимые процессы оказались в начале таблицы и любой процесс был расположен после всех процессов, от которых он зависит. Также в таблицу добавим столбец «Время окончания процесса» и запишем туда длительности независимых процессов.
| A | B | C | D |
|---|
| 1 | ID процесса B | Время выполнения процесса B (мс) | ID процессов A | Время окончания процесса |
|---|
| 2 | 1 | 4 | 0 | 4 |
|---|
| 3 | 2 | 2 | 0 | 2 |
|---|
| 4 | 9 | 7 | 0 | 7 |
|---|
| 5 | 10 | 9 | 0 | 9 |
|---|
| 6 | 4 | 7 | 3 | |
|---|
| 7 | 5 | 6 | 3 | |
|---|
| 8 | 6 | 2 | 5 | |
|---|
| 9 | 8 | 2 | 6 | |
|---|
| 10 | 11 | 6 | 9 | |
|---|
| 11 | 12 | 6 | 10 | |
|---|
| 12 | 3 | 5 | 1;2 | |
|---|
| 13 | 7 | 5 | 4;6 | |
|---|
Далее рассчитаем время выполнения оставшихся процессов:
f(4) = 7 + f(3) = 7 + 9 = 16;
f(5) = 6 + f(3) = 6 + 9 = 15;
f(6) = 2 + f(5) = 2 + 15 = 17;
f(8) = 2 + f(6) = 2 + 17 = 19;
f(11) = 6 + f(9) = 6 + 7 = 13;
f(12) = 6 + f(10) = 6 + 9 = 15;
f(3) = 5 + max(f(1), f(2)) = 5 + 4 = 9;
f(7) = 5 + max(f(4), f(6)) = 5 + 17 = 22.
| A | B | C | D |
|---|
| 1 | ID процесса B | Время выполнения процесса B (мс) | ID процессов A | Время окончания процесса |
|---|
| 2 | 1 | 4 | 0 | 4 |
|---|
| 3 | 2 | 2 | 0 | 2 |
|---|
| 4 | 9 | 7 | 0 | 7 |
|---|
| 5 | 10 | 9 | 0 | 9 |
|---|
| 6 | 4 | 7 | 3 | 16 |
|---|
| 7 | 5 | 6 | 3 | 15 |
|---|
| 8 | 6 | 2 | 5 | 17 |
|---|
| 9 | 8 | 2 | 6 | 19 |
|---|
| 10 | 11 | 6 | 9 | 13 |
|---|
| 11 | 12 | 6 | 10 | 15 |
|---|
| 12 | 3 | 5 | 1;2 | 9 |
|---|
| 13 | 7 | 5 | 4;6 | 22 |
|---|
Построим диаграмму выполнения каждого процесса и рассмотрим когда могут выполняться одновременно 3 процесса.
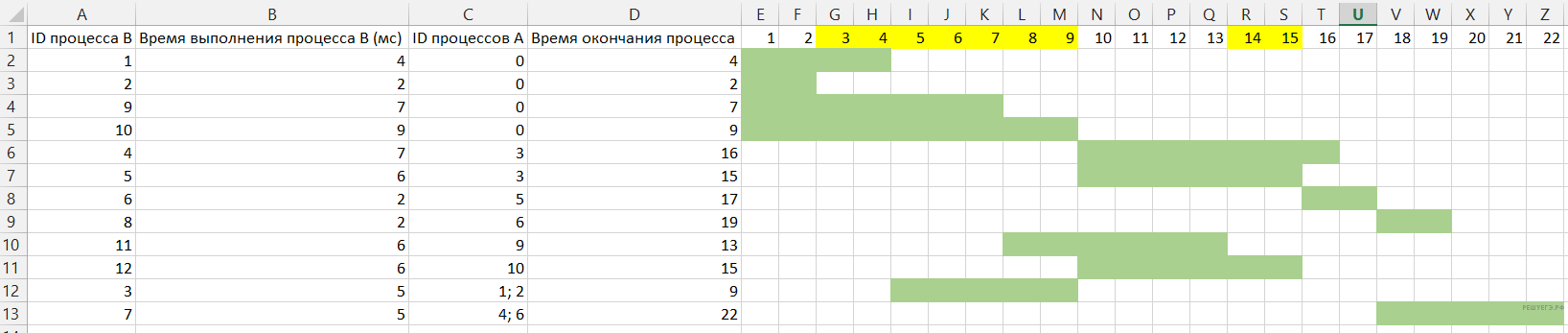
Максимальная продолжительность отрезка времени (в мс), в течение которого возможно одновременное выполнение трёх процессов равна 9.
Ответ: 9.
Приведём решение Юрия Красильникова на языке Python:
Сперва необходимо сохранить содержимое таблицы excel в текстовом файле.
Удаляем из таблицы первую строку с заголовками столбцов. Перед сохранением можно разделить третий столбец на отдельные столбцы с помощью функции «Текст по столбцам», но это необязательно: программа работает и в том, и в другом случае. Выбираем формат сохраняемого файл в Текст CSV. В качестве разделителя полей можно использовать точку с запятой или пробел.
def tstart(p): return 0 if w[p][1] == 0 else max(tstart(i) + w[i][0] for i in w[p][1:])
f=open('221.csv')
lines=[list(map(int,s.replace('»',' ').replace(';',' ').split())) for s in f]
w={line[0]:line[1:] for line in lines}
final=max(tstart(p)+w[p][0] for p in w)
kolp=[sum(1 if tstart(p) <= time < (tstart(p)+w[p][0]) else 0 for p in w) for time in range(final+1)]
print(kolp.count(3)))
Пояснение к программе.
В 3-й строке создается список lines, каждый элемент которого — это список чисел, содержащихся в соответствующей строке текстового файла. Для универсальности все точки с запятой и двойные кавычки в текстовой строке заменяются на пробелы. Для приведенной строки соответствующий элемент списка будет таким: [3, 5, 1, 2].
В 4-й строке из этого списка создается словарь w. Ключ элемента словаря — это номер процесса, а значение — список, состоящий из времени выполнения процесса и номеров процессов, от которых зависит данный процесс. Соответствующий элемент словаря будет выглядеть так: 3:[5, 1, 2].
В 5-й строке вычисляется final — время, через которое завершится выполнение всей совокупности процессов. Это максимум из времени начала каждого процесса из словаря w плюс его продолжительность. (Если мы решаем задачу со стандартным вопросом «Определите минимальное время, через которое завершится выполнение всей совокупности процессов», то значение final — это ответ к такой задаче.)
В 6-й строке строится список kolp. Элемент kolp[0] — это количество процессов, выполняемых в момент времени 0, kolp[1] — их количество в момент 1 и так далее. Значение range(final+1) гарантирует, что мы проведем расчет для всех моментов времени, пока идет выполнение процессов.
В 7-й строке печатается количество элементов списка kolp со значением 3.
Функция tstart(p) вычисляет время начала процесса с номером p. Если процесс независимый (то есть элемент словаря w[p][1]==0), то это время — ноль. Иначе берется максимальное время завершения для всех процессов, от которых зависит данный. Время завершения процесса с номером i — это время его начала плюс его продолжительность (то есть tstart(i)+w[i][0]).
Приведём решение Юрия Красильникова в Excel:
Разобьем списки процессов в столбце C на отдельные числа с помощью функции «Текст по столбцам».
В столбце E у нас будет время начала соответствующего процесса, в столбце F — время его завершения, а в столбцах G и H — времена завершений процессов, от которых зависит данный процесс (номера этих процессов указаны в столбцах C и D).
Впишем в ячейку E2 формулу =МАКС(G2:H2), в ячейку F2 — формулу =E2+B2 и скопируем эти формулы в строки 3-13.
В ячейку G2 впишем формулу =ЕСЛИ(C2>0;ВПР(C2;$A$2:$F$13;6;0);"") и скопируем её во все ячейки диапазона G2:H13.
Теперь определим количество процессов, которые выполняются в каждый момент времени.
Для этого в ячейку A15 запишем 0, в ячейку A16 — 1 и так далее до 30 (можно занести в ячейку А16 формулу =A15+1 и размножить её вниз по столбцу).
В ячейку B15 запишем формулу =СЧЁТЕСЛИМН($E$2:$E$13;"<="&A15;$F$2:$F$13;">"&A15) и размножим её вниз по столбцу B.
Теперь запишем в любую свободную ячейку (например, C15) формулу =СЧЁТЕСЛИ(B15:B45;3) и получим ответ — 9.
 PDF-версии:
PDF-версии: 