Решение. Приведём решение на языке КуМир.

Выберите масштаб сетки равным 1, запустите программу для исполнителя Черепаха.
использовать Черепаха
алг
нач
опустить хвост
нц 2 раз
вперед(14)
влево(270)
назад(12)
вправо(90)
кц
поднять хвост
вперед (9)
вправо(90)
назад (7)
влево(90)
опустить хвост
нц 2 раз
вперед (13)
вправо(90)
вперед (6)
вправо(90)
кц
кон
После выполнения программы считаем точки: 251.
Ответ: 251.
Приведём построение рисунка на языке Python.
from turtle import *
m = 20 # Масштаб
tracer(0)
screensize(5000, 5000) # увеличим размер окна
pd() # опускаем хвост
left(90) # поворачиваем голову в сторону
# положительного направления оси ординат
# Алгоритм
for i in range(2):
forward(14 * m)
left(270)
backward(12 * m)
right(90)
pu() # поднимаем хвост
forward(9 * m)
right(90)
backward(7 * m)
left(90)
pd() # опускаем хвост
for i in range(2):
forward(13 * m)
right(90)
forward(6 * m)
right(90)
pu()# поднимаем хвост
# Проставление точек
for x in range(-10, 100):
for y in range(-10, 110):
goto(x * m, y * m)
dot(3)
done()
Приведём аналитическое решение Александра Козлова.
Формально выполним команды (можно на листе):
Повтори 2 [Вперёд 14 Налево 270 Назад 12 Направо 90]:
Вперёд 14: (0,0)→(0,14) Налево 270°: Назад 12: (0,14)→(-12,14) Направо 90°: теперь направление — вниз (270°).
Вывод: Цикл строит прямоугольник с координатами вершин (0,0),(0,14),(-12,14),(-12,0)
Аналогично выполняем следующие команды: смещаемся в точку с координатами: (-7,9) и строим новый прямоугольник с координатами вершин: (-7, 9), (-7, 22), (-1, 22), (-1, 9)
Для нахождения площади плоскости с рисунком необходимо его высоту умножить на ширину 22 · 12, но нам необходимо найти не площадь, а количество точек, лежащих на его плоскости. Для этого учтем, что на любом отрезке точек всегда больше на 1 следовательно, количество точек на всей плоскости рисунка равно 23 · 13 = 299. Остается по вершинам клеточек подсчитать количество точек не принадлежащих рисунку.
Окончательно получаем 299 – (8*5+8) = 251.
a=0 # находим размер всего рисунка в точках
for x in range(-12, 1):
for y in range(0, 23):
a+=1
b=0 # находим количество исключаемых точек слева от контура рисунка
for x in range(-12, -7):
for y in range(15, 23):
b+=1
c=0 # находим количество исключаемых точек справа от контура рисунка
for x in range(0, 1):
for y in range(15, 23):
c+=1
# находим количество точек лежащих на контуре и внутри его
print(a-(b+c))
Приведём решение Александра Козлова на языке Python.
from turtle import *
m = 12
tracer(0)
lt(90)
for i in range(2):
fd(14 * m)
lt(270)
bk(12 * m)
rt(90)
pu()
fd(9 * m)
rt(90)
bk(7 * m)
lt(90)
pd()
for i in range(2):
fd(13 * m)
rt(90)
fd(6 * m)
rt(90)
pu()
hxs = 0
k = 0
for x in range(-12, 1):
for y in range(0, 23):
hxs += 1
goto(x * m, y * m)
dot(5)
if (x<-7 and y>=15) or (x>-1 and y>=15):
dot(5,'red')
k+=1
print(hxs,' - ',k,' = ',hxs-k)
Приведём решение Юрия Красильникова с помощью электронных таблиц.
Первые пять столбцов озаглавливаем: x, y, угол, движение, поворот. Записываем названия в ячейки A1:E1.
В ячейки A2:C2 записываем начальное состояние черепахи: 0, 0, 90.
Далее заполняем столбцы «движение» и «поворот». В столбец «движение» записываем параметр команды «вперед». Для команды назад пишем её параметр со знаком минус.
В столбец «поворот» записываем параметр команды «направо». Для команды «налево» пишем её параметр со знаком минус.
Таким образом, в одной строке мы задаем сразу две команды: движение и поворот. Если нам нужно что-то одно, то вторым параметром мы указываем 0.
В ячейку A3 записываем формулу =A2+D2*COS(РАДИАНЫ(C2)), в ячейку B3 = формулу =B2+D2*SIN(РАДИАНЫ(C2)), а в ячейку C3 - формулу =ОСТАТ(C2-E2;360). Размножаем эти три ячейки до конца нашей программы и на одну строчку ниже.
Циклы реализуем, записывая группу команд требуемое число раз.
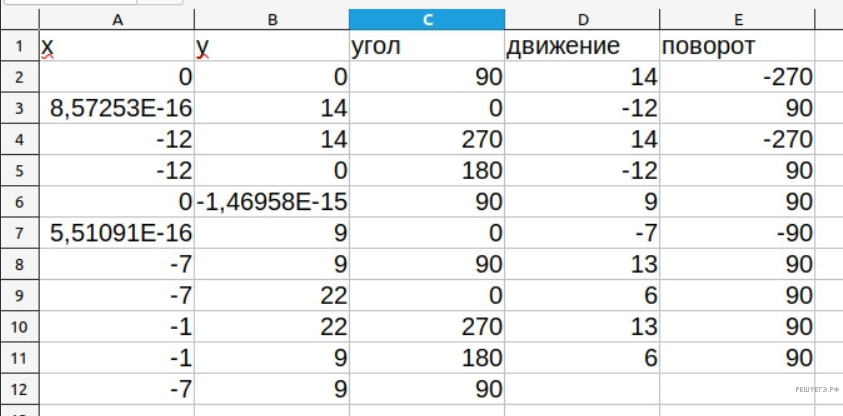
Если построить по первым двум столбцам диаграмму X-Y, «точки и линии», то мы увидим путь черепахи.
Приведём построение рисунка Сергея Донец на PascalABC.NET:
uses turtle;
begin
down;
loop 2 do begin
Forw(14);TurnLeft(270);Forw(-12);TurnRight(90);
end;
up;
Forw(9);TurnRight(90);Forw(-7);TurnLeft(90);
down;
loop 2 do begin
Forw(13);TurnRight(90);Forw(6);TurnRight(90);
end;
end.
 PDF-версии:
PDF-версии: 