Тип Д23 № 6967 
Логические уравнения. Системы логических уравнений со слабо связанными рядами
i
Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?
(x1→x2) ∧ (x2→x3) ∧ (x3→x4) ∧ (x4→x5) = 1
(x1→y1) ∧ (x2→y2) ∧ (x3→y3) ∧ (x4→y4) ∧ (x5→y5) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Решение. Рассмотрим первое уравнение. Логическое «И» истинно, когда истинны все высказывания. Для того, чтобы равенство выполнялось, необходимо, чтобы каждая скобка была истинной. Импликация ложна только тогда, когда посылка истинна, а следствие ложно. Представим решения этого уравнения в виде дерева:
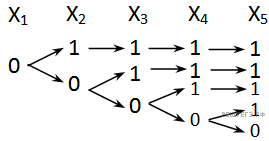
Рассмотрим оставшиееся уравнения для первого набора x1, x2, x3, x4, x5: 11111. Импликация ложна тогда, когда из истинны следует ложь. В данном случае, все x равны 1, следовательно, все y также должны быть равны 1.
Рассмотрим второй набор переменных x1, x2, x3, x4, x5: 01111. Заметим, что все y, кроме первого могут принимать только значения 1, y1 может быть равен 0 или 1. Таким образом, второму набору x соответствует 2 · 1 = 2 набора y.
Рассмотрим третий набор переменных x1, x2, x3, x4, x5: 00111. Заметим, что все y, кроме первого и второго могут принимать только значения 1, y1 и y2 может быть равен 0 или 1. Таким образом, второму набору x соответствует 2 · 2 · 1 = 4 набора y.
Проведя аналогичные рассуждения для наборов x 00011, 00001, 00000, получаем, соответственно 8, 16 и 32 набора y.
Таким образом, получаем 1 + 2 + 4 + 8 + 16 +32 = 63 набора переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств.
Ответ: 63.
Ответ: 63
 PDF-версии:
PDF-версии: 