Тип 22 № 64952 
Многопроцессорные системы. Задания для подготовки
i
В компьютерной системе необходимо выполнить некоторое количество вычислительных процессов, которые могут выполняться параллельно или последовательно. Для запуска некоторых процессов необходимы данные, которые получаются как результаты выполнения одного или нескольких других процессов — поставщиков данных. Если зависимый процесс получает данные от других процессов (поставщиков данных), то выполнение зависимого процесса не может начаться раньше завершения всех процессов-поставщиков. Количество одновременно выполняемых процессов может быть любым, длительность процесса не зависит от других параллельно выполняемых процессов.
В таблице представлены идентификатор (ID) каждого процесса, его длительность и ID поставщиков данных для зависимых процессов. Для независимых процессов в качестве ID поставщика данных указан 0.
Определите максимальную длительность отрезка времени (в мс), в течение которого возможно одновременное выполнение пяти процессов, при условии, что в эту пятёрку не входит процесс с ID = 6.
Выполните задания, используя данные из файла ниже:
Задание 22
Решение. Добавим столбец «Время окончания процесса» и запишем туда длительности независимых процессов.
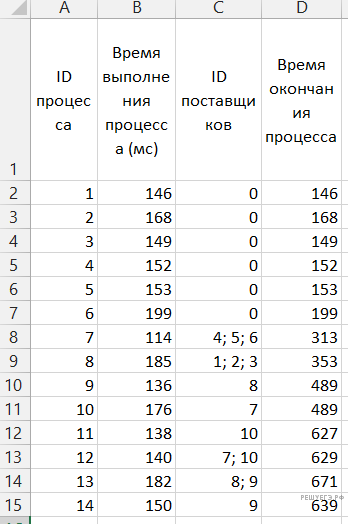
Далее рассчитаем время выполнения оставшихся процессов:
f(7) = 114 + max(f(4), f(5), f(6)) = 313;
f(8) = 185 + max(f(1), f(2), f(3)) = 353;
f(9) = 136 + f(8) = 489;
f(10) = 176 + f(7) = 489;
f(11) = 138 + f(10) = 627;
f(12) = 140 + max(f(7), f(10)) = 629;
f(13) = 182 + max(f(8), f(9)) = 671;
f(14) = 150 + f(9) = 639.
Построим диаграмму выполнения каждого процесса, процесс 6 покрасим красным, а зависимые процессы покрасим в один цвет.

Перенесем зависимые процессы к исходным:

Если не учитывать шестой процесс, то время, когда выполнялись пять процессов равно 146 (процессы с 1 по 5). Попробуем увеличить это время. Процессы, которые не от кого не зависят, можно начинать с любого времени. Пробуем двигать последовательность процессов начинающихся с процессов 1, 2 и 3 к 13 и 14 процессам. Максимальный результат 140.
Если двигать процессы 4, 5 и 6 к процессам 13 и 14, то получим только 4 процесса (так как 6-й процесс не учитывается).
Максимальное время процессов 146 мс. Если рассмотреть другие процессы, то больше времени сделать не получится.
Ответ: 146.
Ответ: 146
 PDF-версии:
PDF-версии: 